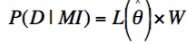The Ockham Factor

In an earlier post, I described how the method of maximum likelihood can deviate radically from the more logical results obtained from Bayes’ theorem, when there is strong prior information available. At the end of that post, I promised to describe another situation where maximum likelihood can fail to capture the information content of a problem, even when the prior distribution for the competing hypotheses is relatively uninformative. Having introduced the foundations of Bayesian model comparison, here, I can now proceed to describe that situation. I’ll follow closely a line of thought developed by Jaynes, in the relevant chapter from ‘Probability theory: the logic of science.’

In parameter estimation we have a list of model parameters, θ, a dataset, D, a model M, and general information, I, from which we formulate

(1)

P(D | θMI) is termed the likelihood function, L(θ | MDI) or more briefly, L(θ). The maximum likelihood estimate for θ is denoted.

When we have a number of alternative models, denoted by different subscripts, the problem of assessing the probability that the j^th model is the right one is just an equivalent one to that of parameter estimation, but carried out at a higher level:

(2)

The likelihood function here makes no assumption about the set of fitting parameters used, and so it decomposes into an integral over the entire available parameter space (extended sum rule, with P(H_iH_j) = 0, for all i ≠ j):

(3)

and the denominator is as usual just the summation over all n competing models, and so we get

(4)

In orthodox hypothesis testing, the weight that a hypothesis is to be given (P(H | DI) for us) is addressed with a surrogate measure: the likelihood function, which is what we would write as P(D | HI). Parameter estimation has never been considered in orthodox statistics to be remotely connected with hypothesis testing, but, since we now recognize that they are really the same problem, we can see that if the merits of two models, M_j and M_k are to be compared, orthodox statistics should do so by calculating the ratio of the likelihood functions at their points of maximum likelihood:

(5)

This, I admit, is something of a straw-man metric – I’m not aware if anybody actually uses this ratio for model comparison, but if we accept the logic of maximum likelihood, then we should accept the logic of this method. (Non-Bayesian methods that attempt to penalize a model for having excessive degrees of freedom, such as the adjusted correlation coefficient, exist, but seem to me to require additional ad hoc principles to be introduced into orthodox probability theory.) Let’s see, then, how the ratio in expression (5) compares to the Bayesian version of Ockham’s razor.

In calculating the ratio of the probabilities for two different models, the denominators will cancel out – it is the same for all models.

Lets express the numerator in a new form by defining the Ockham factor, W (for William, I guess), as follows:

(6)

which is the same as

(7)

from which it is clear that

(8)

Now we can write the ratio of the probabilities associated with the two models, M_j and M_k, in terms of expression (5):

(9)

So the orthodox estimate is multiplied by two additional factors: the prior odds ratio and the ratio of the Ockham factors. Both of these can have strong impacts on the result. The prior odds for the hypotheses under investigation can be important when we already had reason to prefer one model to the other. In parameter estimation, we’ll often see that these priors make negligible difference in cases where the data carry a lot of information. In model comparison, however, prior information of another kind can have enormous impact, even when the data are extremely informative. This is introduced by the means of the Ockham factor, which can easily overrule both the prior odds and the maximum-likelihood ratio.

In light of this insight, we should take a moment to examine what the Ockham factor represents. We can do this in the limit that the data are much more informative than the priors, and the likelihood function is sharply peaked at  (which is quite normal, especially for a well designed experiment). In this case, we can estimate the sharply peaked function L(θ) as a rectangular hyper-volume with a ‘hyper-base’ of volume V, and height . We choose the size of V such that the total enclosed likelihood is the same as the original function:

(10)

We can visualize this in one dimension, by approximating the sharply peaked function below by the adjacent square pulse, with the same area:

Since the prior probability density P(θ | MI) varies slowly over the region of maximum likelihood, we observe that

(11)

which indicates that the Ockham factor is a measure of the amount of prior probability for θ that is packed into the high-likelihood region centered on , which has been singled out by the data. We can now make more concrete how this amount of prior probability in the high likelihood region relates to the ‘simplicity’ of a model by noting again the consequences of augmenting a model with an additional free parameter. This additional parameter adds another dimension to the parameter space, which, by virtue of the fact that the total probability density must be normalized to unity, necessitates a reduction of magnitude of the peak of P(θ | MI), compared to the low-dimensional model. Lets assume that the more complex model is the same as the simple one, but with some additional terms patched in (the parameter sample space for the smaller model is embedded in that of the larger model).  Then we see that it is only if the maximum-likelihood region for the more complex model is far from that of the simpler model, that the Ockham factor has a chance to favor the more complex model.

For me, model comparison is closest to the heart of science. Ultimately, a scientist does not care much about the magnitude of some measurement error, or trivia such as the precise amount of time it takes the Earth to orbit the sun. The scientist is really much more interested in the nature of the cause and effect relationships that shape reality. Many scientists are motivated by desire to understand why nature looks the way it does, and why, for example, the universe supports the existence of beings capable of pondering such things. Model comparison lifts statistical inference beyond the dry realm of parameter estimation, to a wonderful place where we can ask: what is going on here? A formal understanding of model comparison (and a resulting intuitive appreciation) should, in my view, be something in the toolbox of every scientist, yet it is something that I have stumbled upon, much to my delight, almost by chance.   

Fly papers and photon detectors: another base-rate fallacy

Here is my version of a simple riddle posed by Jaynes in ‘Probability Theory: The Logic of Science’:

A constant Poissonian light source emits photons at an average rate of 100 per second. The photons strike a detector with 10% efficiency. In one particular second, the detector registers 15 counts. What is the expectation for the number of photons actually emitted in that second? (Assume a detector with no dark counts and zero dead time.)

Lets denote the number of emissions by n, the average number of emissions (the source strength) by s, the number of detected photons by c, and the detector efficiency by ϕ.

In case some of the terminology in the question is unfamiliar, ‘Poissonian’ just means that the number of events in any second conforms to a Poisson probability distribution with a mean of s:

P(n | s)  =  e-s  sn n!

(1)

Make an effort to work out your best answer to the above question before reading on. Consider writing it down - feel free to record it in the comments below! 


Many textbooks on statistics specify 'maximum likelihood' as the state of the art for parameter estimation, so lets see what result it produces here. The likelihood function for a particular model is the probability to obtain the observed data, assuming that model to be true:

L(M) = P(D | M, I)

(2)

where D is the set of data, M is the model in question, and I is the prior information available.

In the cases where the prior information effectively specifies the form of the model, but not the model parameters, then denoting the parameters of the model by θ, this equation becomes

L(θ) = P(D | θ, I)

(3)

and we have the problem of determining the best estimate of the actual value of the θ from the observed data, which is often assumed to be the value at which the likelihood function is maximized:

^ θ  = argmax(L(θ | D))

(4)

In the present case, θ is a single parameter, the number of emitted photons, n, and D is the fact that we have observed c photocounts. P(D | θI) becomes P(c|nϕs). But if n is known, then knowledge of s is irrelevant, so P(c|nϕs) = P(c|nϕ), which is given by the binomial distribution:

P(c | nφ)  =  n! c!(n - c)!

×  φc (1-φ)n-c

(5)

For ϕ = 0.1 and c  = 15, then it is easy enough to verify that the value of n that maximizes this equation is 150, which is just what many of us would expect.

Lets examine this solution, though, by considering a different problem. Suppose I am interested in the number of flies in Utrecht, the city I live in. I hang a fly paper in my kitchen in order to gather some data (don’t worry, lab experiments on flies don’t require ethical approval). After one day, there are 3 flies trapped. Unfortunately, I don’t know the efficiency of my detector (the fly paper), but suppose I have good reasons to accept that the average number trapped is proportional to the total number in the population. On day 2, I count 6 new casualties on the fly paper, and announce the astonishing result that in one day, the number of flies in Utrecht has doubled. You’d hopefully respond that I am bonkers - clearly the experiment is nowhere near sensitive enough to determine such a thing. Yet this is essentially the result that we have declared above, under the advice of those who champion the method of maximum likelihood for all parameter estimation problems.


The following data are the result of a Monte-Carlo simulation of the emitter and detector described in the original question:

These data represent 32,000 seconds of simulated emissions. First, I generated 32000 random numbers, uniformly distributed between 0 and 1. Then, for each of these, I scanned along the Poisson distribution in equation (1), until the integrated probability first exceeded that random number. This gave the number of emitted photons, n, in each simulated second. Then, for each of these n, I generated another n uniform random numbers. For any of these random numbers less than or equal to the detector efficiency, ϕ, one detected photon was added to the count for that second. Each green dot in the graph above, therefore, displays the emissions and counts for a single second.

The data confirm that 150 emissions in a single second is an extremely rare event (didn’t occur once in the experiment), while 15 photo-counts occurred on very many (more than a thousand) occasions. From the graph above, it appears that the ‘middle’ of the distribution for 15 counts corresponds to somewhere only slightly above 100 emissions. We can get a better view by taking a slice through this graph along 15 counts, and histogramming the numbers of emissions that were responsible for those counts:

The peak of this histogram is at 105 emitted photons, which is also the average number (rounded) of emitted photons resulting in 15 counts. This is evidently our approximate solution.

The exact solution follows from Bayes’ theorem, and has been provided by Jaynes. The general statement of Bayes’ theorem, again, is

P(A | BI)  =  P(A | I)  P(B | AI) P(B | I)

(6)

Filling in the notation I have defined above, this becomes

P(n | φcs)  =  P(n | φs)   P(c | nφs) P(c | φs)

(7)

As noted, if we know the exact number of photons emitted, then no amount of information about the source strength can improve our ability to estimate the expected number of counts. Also, the efficiency of the detector is irrelevant to the number of photons emitted, so

P(n | φcs)  = P(n | s)   P(c | nφ) P(c | φs)

(8)

Two of these distributions are specified above, in equations (1) and (5).

P(n|s) and P(c|nϕ) can be combined to derive the probability distribution for the number of counts given the source strength, which, in line with intuition, is again Poissonian:

P(c | φs)  =  e-sφ  (sφ)c c!

(9)

Combining all these, and canceling terms, we get

P(n | φcs)  =   e-s(1-φ) [ s(1-φ) ] n - c (n-c)!

(10)

This is, yet again, a Poisson distribution, with mean, s(1-ϕ), only shifted up by c, since with no dark counts, the number emitted can not be less than the number detected. The mean of this distribution is, therefore:

〈n〉 =   c + s(1 - φ)

(11)

This gives 15 + 100×0.9 = 105 expected emissions, in the case of 15 detected photons. Counter intuitively, the 5 additional counts, above the expected 10, are only evidence for 5 more photons emitted, above the average.

The figure obtained by maximum likelihood can be seen to be another instance of the base-rate fallacy: 150 is equal to the maximum of P(c|nϕs), as n is varied. This is the essence of what maximum likelihood parameter estimation does - given a model with parameter θ, the maximum likelihood estimate for θ is given by argmax[P(data | θ)]. In this case, it takes no account of the probability distribution for the number of emissions, n. What we really needed was the expectation (approximately the maximum) of P(n | cϕs), which is the expectation of P(n | s)×P(c | nϕs). As with the fly paper, the efficiency of the photo detector, (at 10%) was too low to permit us to claim anything close to a 50% excess over the average 100 emissions per second.

Under the right circumstances, maximum likelihood can do a very good job of parameter estimation, but we see here a situation where it fails miserably. As with all rational procedures, its success is determined entirely by its capability to mimic the results of Bayes’ theorem. The answer it gave here differed from Bayes by an order of magnitude, and the reason for that failure was the important information contained in the base rates, P(n|s). In a future post, I’ll discuss another kind of problem where maximum likelihood can give a badly flawed impression, even when the prior distribution conveys little or no information.