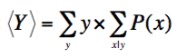Natural Selection By Proxy

Here, I'll give a short summary of one of my favourite studies of recent decades: John Endler's ingenious field and laboratory experiments on small tropical fish¹, which in my (distinctly non-expert) opinion constitute one of the most compelling and 'slam-dunk' proofs available of the theory biological evolution by natural selection. After I've done that, in an act of unadulterated vanity, I'll suggest an extension to these experiments that I feel would considerably boost the information content of their results. That will be what I have dubbed 'selection by proxy'.

Don't get me wrong, Endler's experiments are brilliant. I first read about them in Richard Dawkins' delightful book, 'The Greatest Show on Earth,' and they captured my imagination, which is why I'm writing about them now.

Endler worked on guppies, small tropical fish, the males of which are decorated with coloured spots of varying hues and sizes. Different populations of guppies in the wild were found to exhibit different tendencies with regard to these spot patterns. Some populations show predominantly bright colours, while others prefer more subtle pigments. Some have large spots, while other have small ones. Its easy to contemplate the possibility that these differences in appearance are adaptive under different conditions. Two competing factors capable of contributing a great deal to the fitness of a male guppy are (1) ability to avoid getting eaten by predatory fish, and (2) ability to attract female guppies for baby making. Vivid colourful spots might contribute much to (2), but could be a distinct disadvantage where (1) is a major problem, and if coloration is determined by natural selection, then we would expect different degrees of visibility to be manifested in environments with different levels of predation. And so colour differences might be accounted for.

Furthermore, the idea suggests itself to the insightful observer that in the gravel-bottomed streams in which guppies often live, a range of spot sizes that's matched to the predominant particle size of the gravel in the stream bed would help a guppy to avoid being eaten, and that the tendency for particle and spot sizes to match will be greater where predators are more of a menace, and greater crypsis is an advantage. 

These considerations lead to several testable predictions concerning the likely outcomes if populations of guppies are transplanted to environments with different degrees of predation and different pebble sizes in their stream beds. These predicted outcomes are extremely unlikely under the hypothesis that natural selection is false. Such transplantations, both into carefully crafted laboratory environments, and into natural streams with no pre-existing guppy populations, constituted the punch line of Endler's experiments, and the observed results matched the predictions extraordinarily closely, after only a few months of naturally selected breeding. 

Its the high degree of preparatory groundwork and the many careful controls in these experiments, however, that result in both the high likelihood, P(D_p | H I), for the predicted outcome under natural selection, and the very low likelihood, P(D_p | H' I), under the natural-selection-false hypothesis. These likelihoods, under almost any prior, lead to only one possible logical outcome, when plugged into Bayes' theorem, and make the results conclusive.

The established fact that the patterning of male guppies is genetically controlled served both causes. Of course, natural selection can not act in a constructive way if the selected traits are not passed on to next generation, so the likelihood under H goes up with this knowledge. At the same time, alternate ways to account for any observed evolution of guppy appearance, such as developmental polymorphisms or phenotypic plasticity (such as the colour variability of chameleons, to take an extreme example), are ruled out, hitting P(D_p | H' I) quite hard.

Observations of wild populations had established the types of spot pattern frequent in areas with known levels of predation - there was no need to guess what kind of patterns would be easy and difficult for predators to see, if natural selection is the underlying cause. The expected outcome under this kind of selection could be forecast quite precisely, again enhancing the likelihood function under natural selection.

Selection between genotypes obviously requires the presence of different genotypes to select from, and in the laboratory experiments, this was ensured by several measures leading to broad genetic diversity within the breeding population. This, yet again, increased P(D_p | H I). (Genetic diversity in the wild is often ensured by the tendency for individuals to occasionally get washed downstream to areas with different selective pressures, which is one of the factors that made these fish such a fertile topic for research.)

The experiment employed a 3 × 2 factorial design. Three predation levels (strong, weak, and none) were combined with 2 gravel sizes, giving 6 different types of selection. The production of results appropriate for each of these selection types constitutes a very well defined prediction and would certainly be hard to credit under any alternate hypothesis, and P(D_p | H' I) suffers further at the hands of the expected (and realized) data.

Finally, additional blows were dealt to the likelihood under H', by prudent controls eliminating the possibility of effects due to population density and body size variations under differing predation conditions.

With this clever design and extensive controls, the data that Endler's guppies have yielded offer totally compelling evidence for the role of natural selection. Stronger predation led unmistakably to guppies with less vivid coloration, and greater ability to blend inconspicuously with their environment, after a relatively small number of generations.

I first read about these experiments with great enjoyment, but there was another thing that came to my mind: what the data did not say. It is quite inescapable from the results that natural selection of genetic differences was responsible for observed phenotypic changes arising in populations placed in different environments, but the data say nothing about the mechanism leading to those genetic differences. This, of course, is something that is central to the theory of natural selection. Indeed, we might consider the full name of this theory to be 'biological evolution by natural selection of random genetic mutations.' For the sake of completeness, we would like to have data that speak not only of the natural selection part, but also of the random basis for the genetic transformation.

I'm not saying that there is any serious doubt about this, but neither was there serious doubt about natural selection prior to Endler's result. (In fact, there is some legitimate uncertainty about the relative importance of natural selection v's other processes, such as genetic drift - uncertainty that work of Endler's kind can alleviate.) The theory of biological evolution, though, is a wonderful and extremely important theory. It stands out for a special reason: every other scientific theory we have is ultimately guaranteed to be wrong (though the degree of wrongness is often very small). Evolution by natural selection is the only theory I can think of that in principle could be strictly correct (and with great probability is), and so deserves to have all its major components tested as harshly as we reasonably can. This is how science honours a really great idea.

To test the randomness of genetic mutation, we need to consider alternative hypotheses. I can think of only one with non-vanishing plausibility: that at the molecular level, biology is adaptive in some goal-seeking way. That the cellular machinery strives, somehow, to generate mutations that make their future lineages more suitably adapted to their environment. I'll admit the prior probability is quite low, but I (as an amateur in the field) think its not impossible to imagine a world in which this happens, and as the only remotely credible contender, we should perhaps test it.

We could perform such a test by arranging for natural selection by proxy. That is, an experiment much like Endler's, but with a twist: at each generation, the individuals to breed are not the ones that were selected (e.g. by mates or (passively) by predators), but their genetically identical clones. At each generation, pairs of clones are produced, one of which is added to the experimental population, inhabiting the selective environment. The other clone is kept in selection-free surroundings, and is therefore never exposed to any of the influences that might make goal-seeking mutations work. Any goal-seeking mechanism can only plausibly be based on feedback from the environment, so if we eliminate that feedback and observe no difference in the tendency for phenotypes to adapt (compared to a control experiment executed with the original method), then we have the bonus of having verified all the major components of the theory. And if, against all expectation, there turned out to be a significant difference between the direct and proxy experiments, it would be the discovery of the century, which for its own sake might be worth the gamble. Just a thought.

---

[1]	Natural Selection on Color Patterns in Poecilia reticulata, Endler, J.A., Evolution, 1980, Vol. 34, Pages 76-91 (Downloadable here)

Great Expectations

Thinking ahead to some of the things I'd like to write about in the near future, I expect I'm going to want to make use of the technical concept of expectation. So I'll introduce it now, gently. Some readers will find much of this quite elementary, but perhaps some of the examples will be amusing. This post will be something of a moderate blizzard of equations, and I have some doubts about it, but algebra is important - it's the grease that lubricates the gears of all science. Anyway, I hope you can have some fun with it.

Expectation is just a technical term for average, or mean. It goes by several notations: statisticians like E(X), but physicists use the angle brackets, <X>. As physicists are best, and since E(X) is something I've already used to denote the evidence for a proposition, I'll go with the angle brackets.

We've dealt with the means of several probability distributions, usually denoting them by the Greek letter μ, but how does one actually determine the mean of a distribution? A simple argument should be enough to convince you of what the procedure is. The average of a list of numbers is just the sum, divided by the number of entries in the list. But if some numbers appear more than once in the list, then we can simplify the expression of this sum by just multiplying these by how often they show up. For n unique numbers, x₁, x₂, ..., x_n, appearing k₁, k₂, ..., k_n times, respectively, in the list, the average is given by

(1)

But if we imagine drawing one of the numbers at random from the list, the probability to draw any particular number, x_i, by symmetry is just k_i / (k₁+ k₂ + ... + k_n), and so the expectation of the random variable X is given by

(2)

In the limit where the adjacent points in the probability distribution are infinitely close to one another, this sum over a discrete sample space converts to an integral over a continuum:

(3)

In the technical jargon, when we say that we expect a particular value, we don't quite mean the same thing one usually means. Of course, the actual realized value may be different from what our expectation is, without any contradiction. The expectation serves to summarize our knowledge of what values can arise. In fact, it may even be impossible for the expected value to be realized - the probability distribution may vanish to zero at the expectation if, for example, the rest of the distribution consists of two equally sized humps, equally distant from <X>. (This occurs, for instance, with the first excited state of a quantum-mechanical particle in a box - such a particle in this state is never found at the centre of the box, even though that is the expectation for its position.) This illustrates starkly that it is by no means automatic that the point of expectation is the same as the point of maximum probability.

We can easily extend the expectation formula in an important way. Not only is it useful to know the expectation of the random variable X, but also it can be important to quantify the mean of another random variable, Y, equal to f(X), some function of the first. The probability for some realization, y, of Y is given by the sum of all the P(x) corresponding to the values of x that produce that y:

(4)

This follows very straightforwardly from the sum rule: if a particular value for y is the outcome of our function f operating on any of the x's in the sub-list {x_j, x_k, ...}, then P(y) is equal to P(x_j or x_k or ...), and since the x's, are all mutually exclusive, this becomes P(x_j) + P(x_k) + ....

Noting the generality of equation 2, it is clear that

(5)

which from equation (4) is

(6)

which by distributivity gives

(7)

and since all x map to some y, and replacing y with f(x), this becomes

(8)

which was our goal.

Suppose a random number generator produces integers from 1 to 9, inclusive, all equally probable, what is the expectation for x, the next random digit to come out? Do the sums, verify that the answer is 5. Now, what is the expectation of x²? Perhaps we feel comfortable guessing 25, but better than guessing, lets use equation (8), which we went through so much trouble deriving. The number we want is given by Σ(x²/9), which is 31.667. We see that <x²> ≠ <x>², which is a damn good thing, because the difference between these two is a special number: it is the variance of the distribution for x, i.e. the square of the standard deviation, which (latter) is the expectation of the distance of any measurement from the mean of its distribution. This result is quite general.

As another example, lets think about the expected number of coin tosses, n, one needs to perform before the first head comes up. The probability for any particular n is the probability to get 1 - n tails in a row, followed by 1 head, which is (1/2)ⁿ. We're going to need an infinite sum of these terms, each multiplied by n. There's another fair chunk of algebra following, but nothing really of any difficulty, so don't be put off. Take it one line at a time, and challenge yourself to find a flaw - I'm hoping you won't. I'll start by examining this series:

(9)

multiplying both sides by a convenient factor,

(10)

then removing all terms that annihilate each other, and dividing by that funny factor,

(11)

But p is going to be the probability to obtain a head (or a tail) on some coin toss, so we know it’s less than 1, which means that as n goes to infinity, pⁿ⁺¹ goes to 0, so

(12)

Now the point of this comes when we take the derivative of equation (12) with respect to p:

(13)

Finally, to bump that power of p on the left hand side up from k-1 to k, we just need to multiply by p again, which gives us, from equation (2), the expectation for the number of tosses required to first observe a head:

(14)

Noting that p = 1/2, we find that the expected number of tosses is a neat 2.

Perhaps you already guessed it, but I find this result quite extraordinarily regular. Of all the plausible numbers it could have been, 3.124, 1.583, etc., it turned out to be simple old 2. Quite an exceptionally well behaved system. Unfortunately, all the clunky algebra I've used makes it far from obvious why the result is so simple, but we can generalize the result with a cuter derivation that will also leave us closer to this understanding. We can do this using something called the theorem of total expectation:

(15)

It’s starting to look a little like quantum mechanics, but don’t worry about that. This theorem is both intuitively highly plausible and relatively easy to verify formally. I won't derive it now, but I'll use it to work out the expected number of trials required to first obtain an outcome whose probability in any trial is p. I'll set x equal to the number of trials required, n, and set y equal to the outcome of the first trial:

(16)

The expectation of n, when n is known to be 1 is, not surprisingly, 1. Not only that, but the expectation when n is known to be not 1 is just 1 added to the usual expectation of n since one of our chances out of all those trials has been robbed away: 

(17)

which is very easily solved,

(18)

So the result for the tossed coin, where p = (1 - p) = 0.5, generalizes to any value for p: the expected number of trials required is 1/p. 

Finally a head scratching example, not because of its difficulty (its the simplest so far), but because of its consequences. Imagine a game in which the participant tosses a coin repeatedly until a head first appears, and receives as a prize 2ⁿ dollars, where n is the number of tosses required. This famous problem is known as the St. Petersburg paradox. The expected prize is Σ(2ⁿ/2ⁿ), which clearly diverges to infinity. Firstly, this illustrates that not all expectations are well behaved. Further, the paradox emerges when we consider how much money we should be willing to pay for the chance to participate in this game. Would you be keen to pay everything you own for an expected infinite reward? Why not? Meditation on this conundrum led Daniel Bernoulli to invent decision theory, but how and why will have to wait until some point in the future.