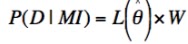The Ockham Factor

In an earlier post, I described how the method of maximum likelihood can deviate radically from the more logical results obtained from Bayes’ theorem, when there is strong prior information available. At the end of that post, I promised to describe another situation where maximum likelihood can fail to capture the information content of a problem, even when the prior distribution for the competing hypotheses is relatively uninformative. Having introduced the foundations of Bayesian model comparison, here, I can now proceed to describe that situation. I’ll follow closely a line of thought developed by Jaynes, in the relevant chapter from ‘Probability theory: the logic of science.’

In parameter estimation we have a list of model parameters, θ, a dataset, D, a model M, and general information, I, from which we formulate

(1)

P(D | θMI) is termed the likelihood function, L(θ | MDI) or more briefly, L(θ). The maximum likelihood estimate for θ is denoted.

When we have a number of alternative models, denoted by different subscripts, the problem of assessing the probability that the j^th model is the right one is just an equivalent one to that of parameter estimation, but carried out at a higher level:

(2)

The likelihood function here makes no assumption about the set of fitting parameters used, and so it decomposes into an integral over the entire available parameter space (extended sum rule, with P(H_iH_j) = 0, for all i ≠ j):

(3)

and the denominator is as usual just the summation over all n competing models, and so we get

(4)

In orthodox hypothesis testing, the weight that a hypothesis is to be given (P(H | DI) for us) is addressed with a surrogate measure: the likelihood function, which is what we would write as P(D | HI). Parameter estimation has never been considered in orthodox statistics to be remotely connected with hypothesis testing, but, since we now recognize that they are really the same problem, we can see that if the merits of two models, M_j and M_k are to be compared, orthodox statistics should do so by calculating the ratio of the likelihood functions at their points of maximum likelihood:

(5)

This, I admit, is something of a straw-man metric – I’m not aware if anybody actually uses this ratio for model comparison, but if we accept the logic of maximum likelihood, then we should accept the logic of this method. (Non-Bayesian methods that attempt to penalize a model for having excessive degrees of freedom, such as the adjusted correlation coefficient, exist, but seem to me to require additional ad hoc principles to be introduced into orthodox probability theory.) Let’s see, then, how the ratio in expression (5) compares to the Bayesian version of Ockham’s razor.

In calculating the ratio of the probabilities for two different models, the denominators will cancel out – it is the same for all models.

Lets express the numerator in a new form by defining the Ockham factor, W (for William, I guess), as follows:

(6)

which is the same as

(7)

from which it is clear that

(8)

Now we can write the ratio of the probabilities associated with the two models, M_j and M_k, in terms of expression (5):

(9)

So the orthodox estimate is multiplied by two additional factors: the prior odds ratio and the ratio of the Ockham factors. Both of these can have strong impacts on the result. The prior odds for the hypotheses under investigation can be important when we already had reason to prefer one model to the other. In parameter estimation, we’ll often see that these priors make negligible difference in cases where the data carry a lot of information. In model comparison, however, prior information of another kind can have enormous impact, even when the data are extremely informative. This is introduced by the means of the Ockham factor, which can easily overrule both the prior odds and the maximum-likelihood ratio.

In light of this insight, we should take a moment to examine what the Ockham factor represents. We can do this in the limit that the data are much more informative than the priors, and the likelihood function is sharply peaked at  (which is quite normal, especially for a well designed experiment). In this case, we can estimate the sharply peaked function L(θ) as a rectangular hyper-volume with a ‘hyper-base’ of volume V, and height . We choose the size of V such that the total enclosed likelihood is the same as the original function:

(10)

We can visualize this in one dimension, by approximating the sharply peaked function below by the adjacent square pulse, with the same area:

Since the prior probability density P(θ | MI) varies slowly over the region of maximum likelihood, we observe that

(11)

which indicates that the Ockham factor is a measure of the amount of prior probability for θ that is packed into the high-likelihood region centered on , which has been singled out by the data. We can now make more concrete how this amount of prior probability in the high likelihood region relates to the ‘simplicity’ of a model by noting again the consequences of augmenting a model with an additional free parameter. This additional parameter adds another dimension to the parameter space, which, by virtue of the fact that the total probability density must be normalized to unity, necessitates a reduction of magnitude of the peak of P(θ | MI), compared to the low-dimensional model. Lets assume that the more complex model is the same as the simple one, but with some additional terms patched in (the parameter sample space for the smaller model is embedded in that of the larger model).  Then we see that it is only if the maximum-likelihood region for the more complex model is far from that of the simpler model, that the Ockham factor has a chance to favor the more complex model.

For me, model comparison is closest to the heart of science. Ultimately, a scientist does not care much about the magnitude of some measurement error, or trivia such as the precise amount of time it takes the Earth to orbit the sun. The scientist is really much more interested in the nature of the cause and effect relationships that shape reality. Many scientists are motivated by desire to understand why nature looks the way it does, and why, for example, the universe supports the existence of beings capable of pondering such things. Model comparison lifts statistical inference beyond the dry realm of parameter estimation, to a wonderful place where we can ask: what is going on here? A formal understanding of model comparison (and a resulting intuitive appreciation) should, in my view, be something in the toolbox of every scientist, yet it is something that I have stumbled upon, much to my delight, almost by chance.   

Ockham's Razor

Numquam ponenda est pluralitas sine necessitate.

- attributed to William of Ockham, circa 1300.

Translation: “Plurality should not be posited without need.”

The above quotation is understood to be a heuristic principle to aid in the comparison of different explanations for a set of known facts.

The principle is often restated as:

          ‘The simplest possible explanation is usually the correct explanation.’

This idea is frequently invoked by scientists, engineers, or any other class of person involved in rational decision making, very often without thinking. We know instinctively, for example, that when trying to identify the cause of the force between two parallel current-carrying wires, it is useless to contemplate the presence of monkeys on the moon. But this is the most trivial form of application of the Ockham principle, specifying our preferred attitude to entities of no conceivable relevance to the subject of study.

Less trivial applications occur when we contemplate things that would have an effect on the processes we study. In such cases it is still widely and instinctively accepted that we should postulate only sufficient causal agents to explain the recorded phenomena. We tend to see the ‘simplicity’ of an explanation, therefore, to be advantageous. Mathematically, this is related to the complexity of the mathematical model with which we formulate our description of a process.  A linear response model, for example, when it gives a good fit, is seen as more desirable than a quadratic model. This may be partly related to the greater ease with which a linear model can be investigated mathematically, but there is also a feeling that if the fit is good, then the linear model probably is the true model, even though the quadratic model will always give a better fit (lower minimized residuals) to noisy data.

Two problems arise if we try to make the Ockham principle objective:

(i)               How do we define the ‘simplicity’ of a model?

(ii)              How are we to determine when it is acceptable to reject a model in

                   favor of one less simple?  

A slightly loose definition of the simplicity of a model is the ease with which it can be falsified. That is, if a model makes very precise predictions, then it is potentially quickly disproved by data, and is considered simple. With a Bernoulli urn, for example, known to contain balls restricted to only 2 possible colours, the theory that all balls are the same colour is instantly crushed, if we draw 2 balls of different hues. An alternate model, however, that the urn contains an equal mixture of balls of both colours is consistent with a wider set of outcomes – if we draw 10 balls, all of the same colour, then it is less likely, but still possible that that there are balls of both colour in the urn.

To make the definition of simplicity more exact, we can say that the simpler model has a less dispersed sampling distribution for the possible data sets we might get if that model is true. P(D | M, I) is more sharply concentrated.

Mathematical models of varying numbers of degrees of freedom can also succumb to a characterization of their relative simplicity using this definition. If one finds that a simple model does not exactly fit the data, then one can usually quite easily ‘correct’ the model by adding some new free parameter, or ‘fudge factor.’ Adding an additional parameter gives the model a greater opportunity to reduce any discrepancies between theory and data, because the sampling distribution for the data is broader – the additional degree of freedom means that a greater set of conceivable observations are consistent with the model, and P(D | M, I) is spread out more thinly. This, however, means that it is harder to falsify the model, and it is this fact that we need to translate into some kind of penalty when we calculate the appropriateness of the model.

To see how we can use Bayes’ theorem to provide an objective Ockham’s razor, I’ll use a beautiful example given by Jeffreys and Berger¹, in ‘Sharpening Ockham’s Razor on a Bayesian Strop.’ The example concerns the comparison of competing theories of gravity in the 1920s: Einstein’s relativity, which we denote by proposition E, and a fudged Newtonian theory, N, in which the inverse-square dependence on distance is allowed instead to become d^-(2+ε), where ε is some small fudge factor. This was a genuine controversy at that time, with some respected theorists refusing to accept relativity. 

The evidence we wish to use to judge these models is the observed anomalous motion of the orbit of Mercury, seen to differ from ordinary Newtonian mechanics by an amount, a = 41.6 ± 2.0 seconds of arc per century. The value, α, calculated for this deviation using E was 42.9’’, a very satisfying result, but we will use our objective methodology to ascertain whether in light of this evidence, E is more probably the truth than N, the fudged Newtonian model. In order to do this we need sampling distributions for the observed discrepancy, a, for each of the models.

For E, this is straightforward (assuming the experimental error magnitude is normally distributed):

For N, the probability to observe any particular value, a, depends not only on the experimental uncertainty, σ, but also on the sampling distribution for α, the predicted value for the anomalous motion. This is because α is not fixed, due to the free parameter, ε. We can treat α as a nuisance parameter for this model:

To find P(α | N), we note that a priori, there is no strong reason for the discrepant motion to be in any given direction, so positive values are as likely as negative ones. Also large values are unlikely, otherwise they would be manifested in other phenomena. From studies of other planets, a value for α > 100’’ can be ruled out. Therefore, we employ another Gaussian distribution, centered at zero and with standard deviation, τ, equal to 50’’.

P(a | N) can then be seen to be a Gaussian determined by the convolution of the measurement uncertainty and the distribution for α:

We’ll consider ourselves to be otherwise completely ignorant about which theory should be favored, and assign equal prior probabilities of 0.5.

Bayes’ theorem in this case is:

and so we get the posterior probabilities: P(E | a, I) = 0.966 and P(N | a, I) =  0.034, which is nearly 30 times smaller. Because the fudged Newtonian theory has 2 uncertainties, the measurement error, and the free parameter, ε, the sampling distribution for the possible observed discrepancy, a, is spread over a much broader range.

Plotting the sampling distributions for the observed value, a, for each of the two models reveals exactly why their posterior probabilities are so different:

Because E packs so much probability into the region close to the observed anomaly, it comes out far more highly favored than N. If the actual observation was far from 40’’, then the additional degree of freedom of model N would be seen to be vindicated.

We can perform a sensitivity analysis to see whether we would have had a radically different result upon choosing a slightly different value for τ. Plotted below are the results for the same probability calculation just performed, but with a large range of possible values of τ:

The result shows clearly that we are not doing a great disservice to the data by arbitrarily setting τ at 50’’. The total absolute variation of P(E | a, I) is less than 0.04. We can also experiment with the prior probabilities, but remarkably, the posterior probability for the Einstein theory, P(E | a, I) falls only to 0.76 if P(E | I) is reduced to 0.1. This illustrates the important point that as long as our priors are somehow reasonably justified, the outcome is very often not badly affected by the slight arbitrariness with which they are sometimes defined.

Note that in order for the posterior probability, P(E | a, I), to be lowered to 0.5, the same value as the prior, we would need to increase the experimental uncertainty, σ, to more than 1000’’. This gives some kind of measure of the large penalty paid by introducing one extra free parameter.

The Ockham principle is a vague rule of thumb that, as we've just seen, can be derived from a much more general and quantitative principle, namely Bayes’ theorem. The fact that many people have been intuitively able to appreciate the validity of Ockham’s razor for roughly seven centuries is suggestive of how close Bayes’ theorem is to the way that human brains perform plausible reasoning. And why should it be any different? Bayes’ theorem is derived from robust logical principles, and it is no surprise that natural selection might favor information processing algorithms that mimic those principles.

In its original informal statement, Ockham’s razor may let us down in some cases, where there is strong prior information, where the ‘simplicity’ of two models is difficult to compare using our ill-defined, intuitive understanding of the term, or where the balance between goodness of fit and the penalty for complexity is too close for intuition alone to judge. The more general application of plausible reasoning using Bayes’ theorem, however, provides the best possible quality of inference, allows all these hard-to-define qualities (prior belief, simplicity, goodness of fit) to be objectively quantified, and puts model comparison on a firm logical basis.

---

[1] W.H. Jeffreys and J.O. Berger, ‘Sharpening Ockham’s Razor on a Bayesian Strop,’ Purdue University technical report #91-44C, August 1991 (Download here.)

The Higgs Boson at 5 Sigmas

Huge congratulations to Peter Higgs and the other theorists who, half a century ago, predicted this particle as part of the standard model, and to the experimentalists at CERN involved in making this recent discovery. We now have extremely compelling evidence of a new particle (new to us, at least) consistent with the Higgs boson. 

Sadly, there's much confusion circulating about the meaning of the 5σ significance level reported for the data on the Higgs. Lets first clear up what this means, before examining some of the confusion.

The null hypothesis, which states that there is no signal present in the data, only noise, implies that the magnitude for some parameter, Y, is some value, μ. Since there is random noise in the data, however, the value of Y observed in a measurement is unlikely to be exactly μ, but will follow a probability distribution with mean μ, and standard deviation σ. If the null hypothesis is true, then we can expect a measurement of Y to produce a result close to μ. The probability is less than 6 × 10^-7 that a measured value will be 5 standard deviations or further from μ, assuming the null hypothesis is true. This number is the p-value associated with the measurement. (In fact, for this case, a single-tailed test was performed, so the reported p-value for the Higgs boson is half this, about 2.8 × 10^-7.)

To recap, the reported p-value is the probability to observe data as extreme as or more extreme than than the data observed, assuming the null hypothesis is true. Roughly speeking, the p-value is P(D | H₀). David Spiegelhalter, over at the Understanding Uncertainty blog, has been monitoring press reports on the recent Higgs announcement, finding a high degree of misunderstanding among the journalists. Many writers described the reported p-value as the probability that the null hypothesis is true, calculated from the data, but this is P(H₀ | D), a very different thing, as I have described before.

Spiegelhalter has found numerous examples of this error, including writers from New Scientist and Nature, who really ought to know better. These are presumably professional journalists, however, who can perhaps be granted some slack, but what about a renowned cosmologist? How about these words:

Each experiment quotes a likelihood of very close to “5 sigma,” meaning the likelihood that the events were produced by chance is less than one in 3.5 million. 

These words come from Lawrence Krauss, a highly respected theoretical physicist, and they are wrong. I mentioned in my very first blog post that physicists are not generally so great at statistics, but I really don't like being proven right so blatantly. I suppose we really mustn't feel too bad about the mistakes in the press, when the experts can't get it right either.

In the article linked above, Spiegelhalter praises a couple of writers for getting the meaning of the p-value the right way round, but really these authors also fail to properly understand the matter. The passages, respectively from the BBC and from the Wall Street Journal, were:

...they had attained a confidence level just at the "five-sigma" point - about a one-in-3.5 million chance that the signal they see would appear if there were no Higgs particle.

and

If the particle doesn't exist, one in 3.5 million is the chance an experiment just like the one announced this week would nevertheless come up with a result appearing to confirm it does exist. 

While both these passages deserve praise for recognizing the p-value as the probability for the data, rather than the probability for the null hypothesis, they unfortunately are still not correct, for a reason that will bring me neatly in a moment to my second major point about the standard of reporting results such as these in terms of p-values. The reason these passages are wrong is that they employ an overly restrictive interpretation of the null hypothesis. They assume H₀ is the same as '"the Higgs boson does not exist," whereas the true meaning is broader: "there is no systematic cause of any patterns present in the data." If we reject the null hypothesis, we still have other possible non-Higgs explanations to rule out before we are sure that the Higgs boson is not a fantasy. These alternatives include other particles, consistent with different physical models; systematic errors in the measurements; and scientific fraud.

This might seem like a subtlety not really worth complaining about, but along with the other errors mentioned, it is a perpetuation of the fallacies surrounding the frequentist hypothesis tests - fallacies that mask the fact that the p-value is a poor summary of a data set, as I have explained in The Insignificance of Significance Tests. Why, for example, is it considered so important to rule out the null hypothesis so comprehensively, when there is little or no attempt to quantify the other alternative hypotheses? The possibility that the observation is a new particle, but not the Higgs, will no doubt be investigated substantially, but presumably will never be presented as a probability. The probability for fraud or systematic error will presumably receive absolutely no formal quantification at all.

Recently, we had a good example of how calculating the probability for measurement error could have prevented substantial trouble. As Ted Bunn has explained, it was a simple matter to estimate this quantity when researchers publicized results suggesting superluminal velocities for neutrinos, yet several groups set up experiments to try to replicate those result, at significant expense, despite the obviousness of the conclusion.

The traditional hypothesis tests set out to quantify, in a rather backwards way, the degree of belief we should have in the null hypothesis, but this is not what we are really interested in. What we want to know when a we look at the results of a scientific study is: what is the probability that the hypothesized phenomenon is real? For this, we should calculate a posterior probability. To do this, we need a specified hypothesis space with an accompanying prior probability distribution. This is one of the things that leads to great discomfort among some statistical thinkers, and was instrumental in leading to the adoption of the p-value as the standard measure of an experiment: how can you obtain a porsterior probability without violating scientific objectivity? How can you assign a prior probability without introducing unacceptable bias into the interpretation of the observations?

The people who think like this, though, don't seem to realize that prior probabilities can be assigned in a perfectly rigorous mathematical way, that will not introduce any unwarranted, subjective degree of belief. There seems to be a feeling like 'we don't know enough to specify the prior probability correctly,' but this is ridiculous - missing knowledge is exactly what probability theory is for. Any probability is just a formally derived, distilled summary of existing information. To calculate the probability for the Higgs, in principle all you need to do is start with a non-informative prior (e.g. uniform), figure out all the relevant information, and bit by bit account for each piece of information using Bayes' theorem. Sure, the bit about figuring out the relevant information is hard, but all those clever particle physicists at CERN must be able, if they put their minds to it. Then it is just a matter of investigating how well the various hypotheses, with and without the Higgs boson, account for various observations, and how efficiently they do so. We'll get a glimpse of how this is done, in a future post, when I get around to discussing model comparison, and a formal implementation of Ockham's razor.

Yes, there will always need to be assumptions made, in order to carry out such a program, but inductive inference is impossible without assumptions, (if you don't believe me, try it!) and any competent scientist (almost by definition) will be able to keep the assumptions used to those that either are accepted by practically everybody, or make negligible difference to the result of the calculation. It is the frequentists who are committing a fallacy by trying to learn in a vacuum.

I find it a great pity that the posterior distribution was not the chosen route taken for reduction of the data from the Large Hadron Collider. Firstly, this is an extremely fundamental question, and if any question deserves the best possible answer from the available data, this is it. The p-value simply doesn't extract all the information from the observations we now have at our disposal. Secondly, yes: it is a hugely complicated problem to assign a prior probability to a hypothesis like this, but this is a project involving a huge number of presumably some of the finest scientific minds around - if anybody can do it, they can. If they did, it would first of all prove that it can be done, and secondly it would lay a very strong foundation for the development of general techniques and standards for the computation of all manner of difficult-to-obtain priors.